The power of likelihood in theory

Research Software & Analytics Group, University of Exeter
June 4th, 2025
Mass modeling: parametric, non-linear, multi-phase models
Source reconstruction: linear, reconstructing unlensed light distribution via different kinds of meshes: rectangular, Delaunay, Voronoi
Log-likelihood function takes the output of (1) and computes its likelihood (where (2) is part of the calculation).
Key goal is to automate the whole process and apply it to large datasets.

PyAutoLens (via PyAutoFit) supports Nested sampling (Dynesty), MCMC (emcee), particle swarm optimization (PySwarms)
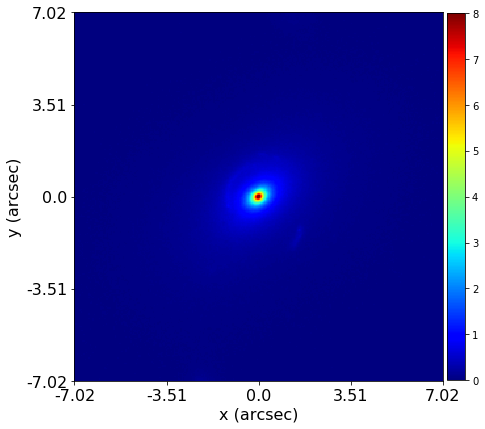
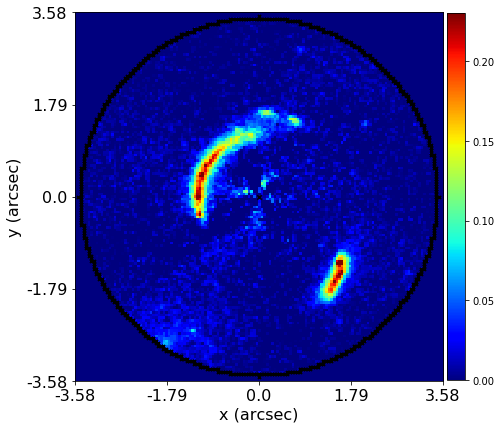
PyAutoLens (via PyAutoFit) supports Nested sampling (Dynesty), MCMC (emcee), particle swarm optimization (PySwarms)
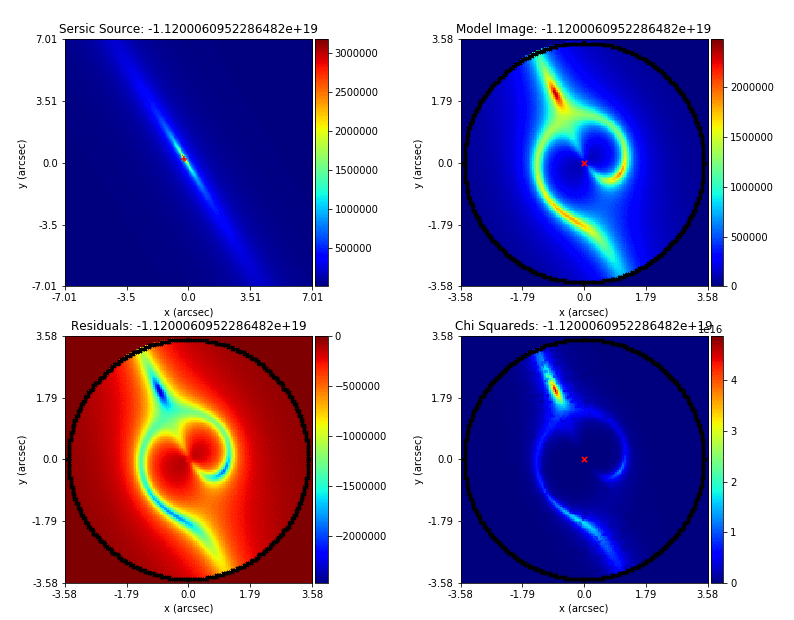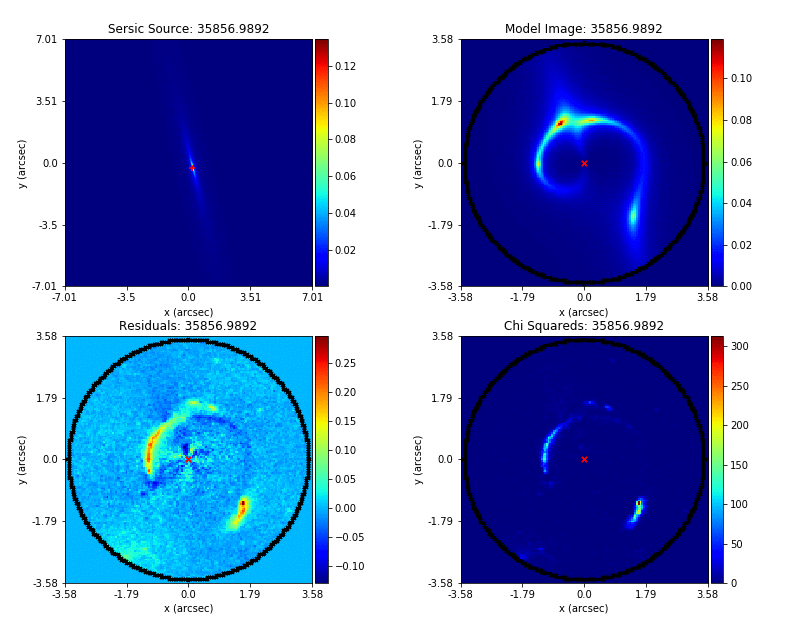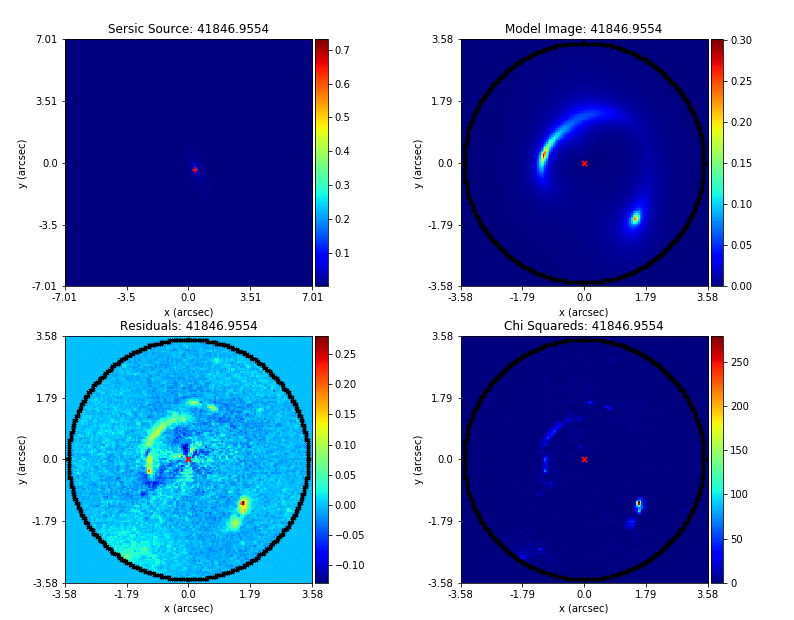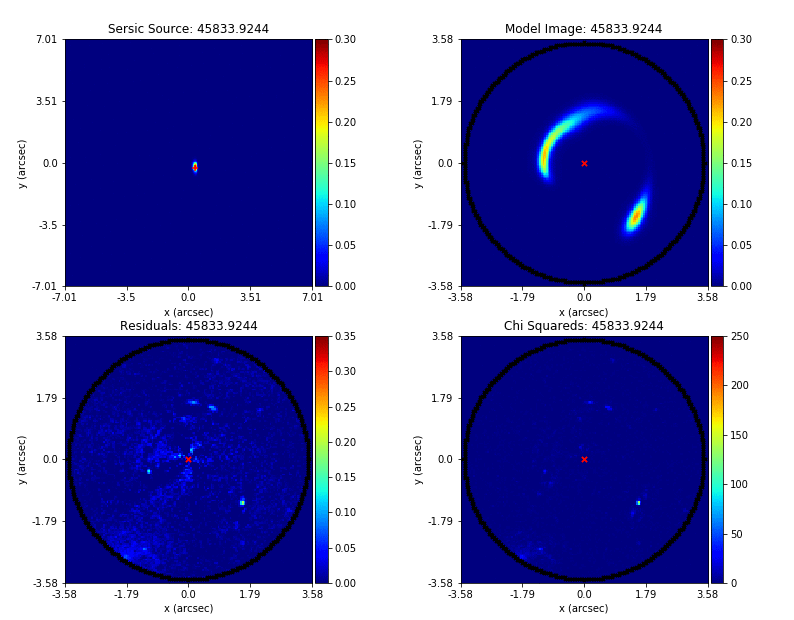

original for the original functions, numba for
those ported in (2), jax for those ported in (3)| Numba | JAX |
|---|---|
| C-like mini language | Smaller language (\(\text{JAX} \underset{\sim}{\subset} \text{Numba}\)): restrictions on control flow, mutation, and dynamic shapes |
| Implements a subset of Python+NumPy, with a parallelization model similar to a mini-“OpenMP” | Implements a subset of Python+NumPy+SciPy exposed via duck-typing. |
| NumPy implementations are dropped in replacement but only a subset is implemented. Calling NumPy within jitted function is completely hijacked. Documentation is minimal. | jax.numpy
and jax.scipy
have similar API comparing to NumPy and SciPy, but has its own
documentation. This facilitates deviations
in behaviors. |
| Functions “recompile” whenever input type changes. | Functions “recompile” whenever input type and shape changes. |
| No automatic compiling & offloading to accelerator. No autograd/autodiff. | Going through FFI is more costly: memory transfer from and to device, losing autograd/autodiff. |
tracing compiler & recompile per shape change \(\Rightarrow\)
static_argnums
Compiler Driven Design
Easy to port to GPU without setting one up.
JAX vs numba-cuda: The XLA compiler handles device-specific optimization automatically.
JAX nudges you to write correct code, and performance comes as a bonus.
\[\tilde{W}_{ij} = \sum_{k=1}^K \frac{1}{n_k^2} \cos(2\pi[(g_{i1} - g_{j1})u_{k0} + (g_{i0} - g_{j0})u_{k1}])\]
@numba.jit(nopython=True, nogil=True, parallel=True)
def w_tilde_curvature_interferometer_from(
noise_map_real: np.ndarray,
uv_wavelengths: np.ndarray,
grid_radians_slim: np.ndarray,
) -> np.ndarray:
w_tilde = np.zeros((grid_radians_slim.shape[0], grid_radians_slim.shape[0]))
for i in range(w_tilde.shape[0]):
for j in range(i, w_tilde.shape[1]):
y_offset = grid_radians_slim[i, 1] - grid_radians_slim[j, 1]
x_offset = grid_radians_slim[i, 0] - grid_radians_slim[j, 0]
for vis_1d_index in range(uv_wavelengths.shape[0]):
w_tilde[i, j] += noise_map_real[vis_1d_index] ** -2.0 * np.cos(
2.0
* np.pi
* (y_offset * uv_wavelengths[vis_1d_index, 0] + x_offset * uv_wavelengths[vis_1d_index, 1])
)
for i in range(w_tilde.shape[0]):
for j in range(i, w_tilde.shape[1]):
w_tilde[j, i] = w_tilde[i, j]
return w_tilde\[\tilde{W}_{ij} = \sum_{k=1}^K \frac{1}{n_k^2} \cos(2\pi[(g_{i1} - g_{j1})u_{k0} + (g_{i0} - g_{j0})u_{k1}])\]
@jax.jit
def w_tilde_curvature_interferometer_from(
noise_map_real: np.ndarray[tuple[int], np.float64],
uv_wavelengths: np.ndarray[tuple[int, int], np.float64],
grid_radians_slim: np.ndarray[tuple[int, int], np.float64],
) -> np.ndarray[tuple[int, int], np.float64]:
# (M, M, 1, 2)
g_ij = grid_radians_slim.reshape(-1, 1, 1, 2) - grid_radians_slim.reshape(1, -1, 1, 2)
# (1, 1, K, 2)
u_k = uv_wavelengths.reshape(1, 1, -1, 2)
return (
jnp.cos(
(2.0 * jnp.pi) *
# (M, M, K)
(
g_ij[:, :, :, 0] * u_k[:, :, :, 1] +
g_ij[:, :, :, 1] * u_k[:, :, :, 0]
)
) /
# (1, 1, K)
jnp.square(noise_map_real).reshape(1, 1, -1)
).sum(2) # sum over k\[\tilde{W}_{ij} = \sum_{k=1}^K \frac{1}{n_k^2} \cos(2\pi[(g_{i1} - g_{j1})u_{k0} + (g_{i0} - g_{j0})u_{k1}])\]
@jax.jit
def w_tilde_curvature_interferometer_from(
noise_map_real: np.ndarray[tuple[int], np.float64],
uv_wavelengths: np.ndarray[tuple[int, int], np.float64],
grid_radians_slim: np.ndarray[tuple[int, int], np.float64],
) -> np.ndarray[tuple[int, int], np.float64]:
# A_mk, m<M, k<K
# assume M > K to put TWO_PI multiplication there
A = grid_radians_slim @ (TWO_PI * uv_wavelengths)[:, ::-1].T
noise_map_real_inv = jnp.reciprocal(noise_map_real)
C = jnp.cos(A) * noise_map_real_inv
S = jnp.sin(A) * noise_map_real_inv
return C @ C.T + S @ S.T\[\tilde{W}_{ij} = \sum_{k=1}^K \frac{1}{n_k^2} \cos(2\pi[(g_{i1} - g_{j1})u_{k0} + (g_{i0} - g_{j0})u_{k1}])\]
\((M, M, K, 2)\) of 64-bit array would be \(\sim 700\) PiB!
While \((M, M)\) of 64-bit array would be \(\sim 40\) GiB only.
\[\tilde{W}_{ij} = \sum_{k=1}^K \frac{1}{n_k^2} \cos(2\pi[(g_{i1} - g_{j1})u_{k0} + (g_{i0} - g_{j0})u_{k1}])\]
@numba.jit("f8[:, ::1](f8[::1], f8[:, ::1], f8[:, ::1])", nopython=True, nogil=True, parallel=True)
def w_tilde_curvature_interferometer_from(
noise_map_real: np.ndarray[tuple[int], np.float64],
uv_wavelengths: np.ndarray[tuple[int, int], np.float64],
grid_radians_slim: np.ndarray[tuple[int, int], np.float64],
) -> np.ndarray[tuple[int, int], np.float64]:
M = grid_radians_slim.shape[0]
K = uv_wavelengths.shape[0]
g_2pi = TWO_PI * grid_radians_slim
δg_2pi = g_2pi.reshape(-1, 1, 2) - g_2pi.reshape(1, -1, 2)
w = np.zeros((M, M))
for k in numba.prange(K):
w += np.cos(δg_2pi[:, :, 1] * uv_wavelengths[k, 0] + δg_2pi[:, :, 0] * uv_wavelengths[k, 1]) * np.reciprocal(
np.square(noise_map_real[k])
)
return w@jax.jit
def w_tilde_curvature_interferometer_from(
noise_map_real: np.ndarray[tuple[int], np.float64],
uv_wavelengths: np.ndarray[tuple[int, int], np.float64],
grid_radians_slim: np.ndarray[tuple[int, int], np.float64],
) -> np.ndarray[tuple[int, int], np.float64]:
M = grid_radians_slim.shape[0]
g_2pi = TWO_PI * grid_radians_slim
δg_2pi = g_2pi.reshape(M, 1, 2) - g_2pi.reshape(1, M, 2)
δg_2pi_y = δg_2pi[:, :, 0]
δg_2pi_x = δg_2pi[:, :, 1]
def f_k(
noise_map_real: float,
uv_wavelengths: np.ndarray[tuple[int], np.float64],
) -> np.ndarray[tuple[int, int], np.float64]:
return jnp.cos(δg_2pi_x * uv_wavelengths[0] + δg_2pi_y * uv_wavelengths[1]) * jnp.reciprocal(
jnp.square(noise_map_real)
)
def f_scan(
sum_: np.ndarray[tuple[int, int], np.float64],
args: tuple[float, np.ndarray[tuple[int], np.float64]],
) -> tuple[np.ndarray[tuple[int, int], np.float64], None]:
noise_map_real, uv_wavelengths = args
return sum_ + f_k(noise_map_real, uv_wavelengths), None
res, _ = jax.lax.scan(
f_scan,
jnp.zeros((M, M)),
(
noise_map_real,
uv_wavelengths,
),
)
return res| Implementation | s | σ |
|---|---|---|
jax_compact_expanded |
2.5535 (1.0) | 0.0032 |
jax_compact |
2.5543 (1.00) | 0.0050 |
numba_compact |
2.8768 (1.13) | 0.0012 |
numba_compact_expanded |
2.8967 (1.13) | 0.0004 |
original_preload |
11.0392 (4.32) | 0.0010 |
original_preload_expanded |
11.0686 (4.33) | 0.0005 |
jax |
3,368.6229 (>1000.0) | 1.6803 |
original |
3,561.0805 (>1000.0) | 0.2255 |
numba |
3,702.7006 (>1000.0) | 0.7385 |
| Implementation | ms | σ |
|---|---|---|
numba_compact |
2.5029 (1.0) | 0.0520 |
numba_compact_expanded |
3.7808 (1.51) | 0.0415 |
jax_compact_expanded |
58.6799 (23.44) | 9.1624 |
jax_compact |
61.5560 (24.59) | 6.8555 |
jax |
143.2451 (57.23) | 0.0749 |
original_preload |
840.0727 (335.63) | 0.1761 |
original_preload_expanded |
842.6588 (336.67) | 0.4933 |
numba |
1,794.1949 (716.83) | 14.9648 |
original |
69,304.2738 (>1000.0) | 13.5543 |
\[F = T^T \tilde{w} T\]
| Implementation | ms | σ |
|---|---|---|
numba_sparse |
8.0733 (1.0) | 0.0501 |
jax |
19.7302 (2.44) | 1.6986 |
jax_sparse |
25.0091 (3.10) | 0.1484 |
jax_BCOO |
48.5340 (6.01) | 0.1571 |
numba_compact_sparse |
49.8400 (6.17) | 0.0794 |
original_preload_direct |
99.2061 (12.29) | 0.3163 |
numba |
125.3019 (15.52) | 0.1143 |
original |
132.4863 (16.41) | 0.1376 |
numba_compact_sparse_direct |
139.9244 (17.33) | 0.1562 |
jax_compact_sparse_BCOO |
379.7214 (47.03) | 1.4144 |
jax_compact_sparse |
380.8865 (47.18) | 2.4322 |
| Implementation | μs | σ |
|---|---|---|
jax |
260.5957 (1.0) | 29.3714 |
jax_BCOO |
3,078.2068 (11.81) | 35.9463 |
jax_compact_sparse_BCOO |
3,207.3388 (12.31) | 107.0798 |
numba_sparse |
5,548.5175 (21.29) | 64.3711 |
jax_compact_sparse |
7,190.9015 (27.59) | 35.7355 |
numba |
18,187.5003 (69.79) | 5,603.6081 |
original |
18,279.9851 (70.15) | 6,052.1386 |
jax_sparse |
19,786.7200 (75.93) | 42.9344 |
numba_compact_sparse |
32,605.2243 (125.12) | 248.8764 |
numba_compact_sparse_direct |
1,362,329.9249 (>1000.0) | 1,366.9112 |
original_preload_direct |
25,218,633.7856 (>1000.0) | 8,722.4870 |
JAX for multithreading on the CPU is a rabbit hole. All links below are from GitHub issues. The lack of documentation reflects on the lack of interest in multicore parallelism on the CPU from the primarily machine learning community (JAX from Google, XLA from OpenXLA).
From JAX running in CPU only mode only uses a single core:
This is largely working as intended at the moment. JAX doesn’t parallelize operations across CPU cores unless you use explicit parallelism constructs like pmap. Some JAX operations (e.g., BLAS or LAPACK) operations have their own internal parallelism.
In an HPC setting, you may want to use multiple hierarchies of
parallelism on the CPU: SIMD + Multi-threading (e.g. OpenMP) +
Multi-processing (e.g. MPI). In this case, you’d want to limit the
number of CPU cores for multi-threading, often set via
..._NUM_THREADS. This is very obscure in how to achieve
such in JAX:
XLA_FLAGS='--xla_cpu_multi_thread_eigen=false intra_op_parallelism_threads=1'
was
the recommendation. It
is now recommended to use NPROC=1 to disable
multithreading used in Eigen instead. Notice the lack of
JAX_NUM_THREADS \(\Rightarrow\) NPROC might have
side-effects.export MKL_NUM_THREADS=${NUM_THREADS}
export MKL_DOMAIN_NUM_THREADS="MKL_BLAS=${NUM_THREADS}"
export MKL_DYNAMIC=FALSE
export OMP_NUM_THREADS=${NUM_THREADS}
export OMP_PLACES=threads
export OMP_PROC_BIND=spread
export OMP_DYNAMIC=FALSE
export NUMEXPR_NUM_THREADS=${NUM_THREADS}
export OPENBLAS_NUM_THREADS=${NUM_THREADS}
export NUMBA_NUM_THREADS=${NUM_THREADS}
export NPROC=${NUM_THREADS}
export JAX_NUM_CPU_DEVICES=1
export TF_NUM_INTEROP_THREADS=1
export TF_NUM_INTRAOP_THREADS=${NUM_THREADS}You may set JAX_NUM_CPU_DEVICES=${NUM_THREADS}
instead, together with sharding to shard your array to different CPU
cores. I.e. OpenMP-like parallelism cannot be achieved. Also,
jax.device_put requires your array length is divisible by
JAX_NUM_CPU_DEVICES.
originalnumbajax